(a)	(b)
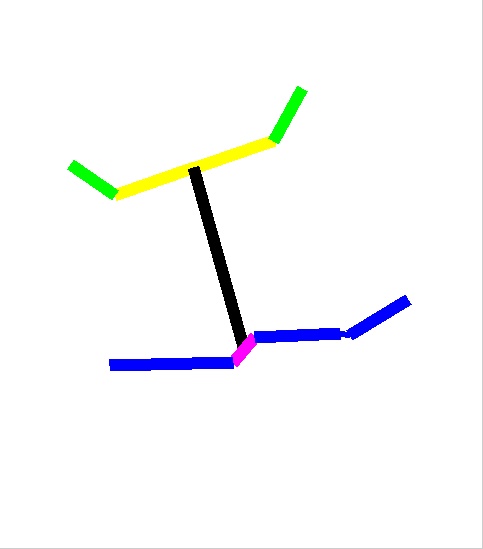
Figure 1: the challenge is to take an input image (a), and recover the body configuration in (b), without any assumptions about pose, clothing, scale or background clutter.

The goal of this work is to take an image such as the one in Figure 1(a), detect a human figure, and find the configuration of parts (b). This is a very difficult problem, partly because human bodies are versatile, presenting a wide range of pose and aspects, many including self-occlusion, and partly because variations in clothing and background clutter deny a simple appearance model.

We tackle this problem by explicitly detecting body parts from bottom-up and then assembling them into configurations Without restrictions in pose, appearance, or background clutter, a tree-based model no longer suffices (cf the discussions in our earlier paper on segmentation-based people finding). Additional sources of information, not provided by tree based models, are required to succeed. For example, the symmetry of clothing is a powerful cue to constrain limb appearance. As another example, in Figure 1, what reveals the body position to us are the connection between the two upper legs and the relative geometric relationship between arms and legs, both of which are not in the traditional tree-based model.

It is an open question what models can express sufficient constraints and are computationally feasible. In this work, we develop a strategy that exploits a rich set of cues, defined on arbitrary pairs of parts, to constrain body configurations. We learn these constraints from empirical data and use Integer Quadratic Programming (IQP) to find the most probable configurations. The IQP framework allows incorporating much more information than dynamic programming on trees, and can handle a much larger set of candidate parts than a brute-force search strategy.

Our approach is outlined in the following figure:

(a)	(b)	(c)
(d)	(e)	(f)
Figure 2: the processing pipeline. Given an input image (a), compute an edge map (b), break this into segments and compute a constrained Delaunay triangulation (c), identify part candidates by exploiting parallelism of part boundaries (d), find a good configuration using Integer Quadratic Programming over pairwise constraints between body parts (e), use the labeled segments and stick figure to find an approximate segmentation of the figure (f).

Detecting Parts using Parallelism

Our part detector is based on the following key observation: parts of a human body, or of an articulated object in general, are mostly characterized by a pair of parallel line segments. Parallelism or Ebenbreite, known from the early days of the Gestalt movement, is a fundamental principle in human vision and its perception is commonly known to occur early in the visual pathway.

We start with the construction of the Constrained Delaunay Triangulation graph from bottom-up. This gives us a discrete graph of approximately straight edge segments. Then we train a logistic classifier on a pair of edge elements to compute the probability of them forming the boundary of a body part. The features we use for parallelism include angles, line length and alignment of centers.

(a)	(b)
Figure 3: detecting parts from bottom-up, using a logistic classifier on the basis of a discrete CDT graph representation. (a) shows the (color-coded) top 10 part candidates in the example image, and (b) shows all the candidates.

One advantage of using the CDT graph for part detection is that it is scale-invariant. We do not make any assumption about the absolute scale of the parts. Long horizon lines remain undivided in the CDT graph, and they form a single candidate. Consequently, there are only about one hundred candidates, in total, in the example image. This is in sharp contrast with top-down approaches, where one may have to consider millions of possibilities, searching over position, orientation and scale.

Pairwise Constraints between Body Parts

Without any assumption about the appearance of body parts, it is impossible to detect them in separation. As we can see in Figure 3, there are a lot of false positive detections. The nature of the problem is such that, compare to low-level saliency, global configuration consistency is much more important.

How do we model the global configuration consistency?

Given the set of candidates {c_i}, we try to assign to them a set of part labels {l_i}, where {l_i} are from the canonical 9-part body model (torso plus 8 half-limbs). For a pair of label assignments (l₁,c₁,l₂,c₂), we use the following set of constraints:

• scale consistency: although length of a part could be foreshortened, width is a reliable estimate of its scale, and if we label one candidate part as torso and another as upper arm, the relative widths of these two candidates have to be compatible (as dictated by their labels).
• appearance consistency: brightness/color are similar to each other for some pairs of parts (such as between the two lower legs) but not others.
• orientation consistency: for some pairs of parts (such as upper leg and lower leg), the difference between their orientations tends to be small, and rarely more than 90 degrees.
• connectivity: the connectivity constraint includes the adjacency between adjacent body parts in a tree model (most commonly used cues in body configuration, such as between torso and upper leg), the V-shape cue (i.e. the adjacency between two upper legs) and smooth connection between non-adjacent parts (e.g. arms and legs should be connected by a smooth path of edges; this is useful when toro or other parts are missing or cannot be reliably detected).

It is worth noting that we include a few non-traditional configuration cues in our model, such as V-shape, symmetry of appearance, and connectivity between non-adjacent parts. Preliminary quantitative analysis shows that these cues contain a significant amount of information about body configuration. Such constraints, however, are not in a tree model and cannot be exploited by dynamic programming. Instead we use an Integer Quadratic Programming formulation, where arbitrary pairwise constraints can be incorporated.

Correspondence with Integer Quadratic Programming (IQP)

Suppose that there are m candidates (m ≈ 100) and n labels (n=9). Let x be a binary vector of length (mn) which indicates the assignment of labels to candidates. The pairwise constraints above can be written down in a quadratic form, and to find the best configuration we solve the following quadratic program:

min Q(x) = x' H x + c' x

s.t. A x= b

where H encodes the pairwise assignment costs, c encodes unary costs, and A specifies the constraints that x is a valid assignment (i.e. there is a only one assignment for each label).