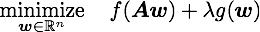
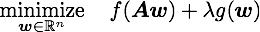
DAL solves the dual problem of (1) via the augmented Lagrangian method (see Bertsekas 82). It uses the analytic expression (and its derivatives) of the following soft-thresholding operation:
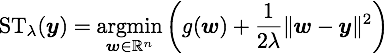
which can be computed for L1 and grouped L1 (and many other) sparsity inducing regularizers. If you are interested in our algorithm please find more details in our JMLR paper or in my talk at Optimization for Machine Learning Workshop (NIPS 2009).
For L1 regularized regression (aka lasso):
[xx,status]=dalsql1(zeros(n,1), A, bb, lambda);
A (m x n) is the design matrix, bb (m x 1) is the target vector, and lambda is the regularization constant. xx is the regression coefficient (solution) and the first argument of dalsql1 is its initial value.
For grouped L1 regularized regression (aka group lasso):
[xx,status]=dalsqgl(zeros(ns,nc), A, bb, lambda);
A (m x n or m x ns x nc with ns*nc=n), bb (m x 1), and lambda are defined as above. xx is the regression coefficient (solution) and the first argument of dalsqgl is its initial value.
When the initial xx is given as a matrix (as above), dalsqgl assumes nc groups of size ns. In order to specify non-equal-sized groups, you can specify the option blks as follows:
[xx,status]=dalsqgl(zeros(n,1), A, bb, lambda, 'blks', [10 10 20]);
xx is a (n x 1)-vector. Note that you might need to normalize the data appropriately to make groups of different sizes comparable to each other.
For L1 regularized logistic regression:
[xx,bias,status]=dallrl1(zeros(n,1), 0, A, yy, lambda);
A (m x n) is the design matrix, yy (m x 1) is the target vector (-1 or +1), and lambda is the regularization constant. Note that the bias term is not regularized. xx (n x 1) and bias are the classifier weight vector and the bias, respectively, and the first two arguments of dalsql1 are their initial values.
See more examples on the github page.
DAL is provided through the MIT license, i.e., free to include this software in any (non-open) project as long as the copyright information is kept. We kindly ask you to cite our paper when you publish something based on this software.
Copyright (c) 2009 Ryota Tomioka
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
I am happy to receive any kind of feedbacks (bugs, comments, etc).
E-mail: tomioka mist.i.u-tokyo.ac.jp
mist.i.u-tokyo.ac.jp
