Bayesian Inference in Large-Scale Sparse Models: Efficient Monte-Carlo and Variational Approaches
Overview
|
|
We study linear models under heavy-tailed priors from a probabilistic viewpoint. Instead of computing a single sparse most probable (MAP) solution as in standard deterministic techniques, the focus in the Bayesian compressed sensing framework shifts towards capturing the full posterior distribution on the latent variables. This allows quantifying the estimation uncertainty and learning model parameters using maximum likelihood. The exact posterior distribution under the sparse linear model is intractable and we propose both Monte-Carlo and variational Bayesian methods to approximate it. Efficient Gaussian sampling by local perturbations turns out to be a key computational module that allows both of these classes of algorithms to handle large-scale datasets with essentially the same memory and time complexity requirements as conventional MAP estimation techniques. We experimentally demonstrate these ideas in Bayesian total variation (TV) signal estimation, visual receptive field learning, and blind image deconvolution, among other applications. |
Efficient Monte-Carlo Inference in Sparse Models (NIPS-10 paper)
Fast sampling in sparse models: Conditionally Gaussian modeling and block Gibbs sampling
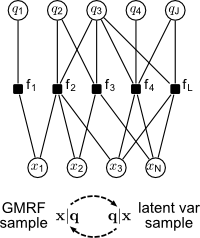 |
Key for efficient sampling in sparse models is the observation that the MRF
non-quadratic potentials coupling the different variables Using this representation, we can design an efficient block Gibbs sampler which alternately draws samples of the conditionally independent latent mixture assignments and the conditionally multivariate Gaussian continuous vector, as shown in the box to the left. The conditionally Gaussian sampling step can be carried out fast even in large-scale models by using the Gaussian sampling by local perturbations algorithm, as described in our Perturb-and-MAP page. Closely related work is carried out in the group of S. Roth at TU Darmstadt. |
Application: TV signal restoration under the MMSE criterion
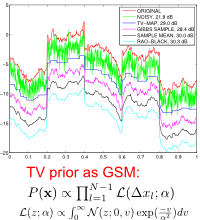 |
As a demonstration of these ideas, consider the problem of signal restoration under a total variation (TV) prior. We can express the Laplacian potentials in the TV model as Gaussian scale mixtures (GSMs), with each latent variance variable following an exponential distribution. This leads to a fast mixing block Gibbs sampling algorithm which allows us estimate the posterior mean of the latent underlying signal from noisy measurements. The posterior mean estimator is optimum with respect to the MMSE criterion and is also free of the staircasing artifacts of the standard MAP estimator. Although inferior in terms of PSNR performance, individual posterior samples are also interesting since they reproduce the texture of the underlying signal. See the figure on the left (zoom). |
Application: Learning image receptive fields
 |
We have successfully employed the block-Gibbs sampler in the context of unsupervised learning of hierarchical models applied on real-valued data, where it is natural to use a Gaussian Boltzmann machine with sideways connections between the continuous visible units in the first layer of the hierarchy. The figure on the left illustrates the receptive fields learned by maximum likelihood from a dataset of natural images using the proposed techniques. |
Efficient Variational Bayesian Inference (ICCVW-11 paper)
Variational bounding and expectation propagation
 |
An alternative to MCMC for inference is through variational Bayesian techniques. The strategy here is to approximate the intractable posterior distribution with a simplified parametric form and adjust the variational parameters so as to optimize the fit – see Figure to the left. Methods such as variational bounding (VB) and expectation propagation (EP) fall within this framework. Compared to MCMC, the price one has to pay with variational approximations is that they introduce a systematic error in the inference process. However, they involve solving an optimization problem (often a convex one) thus avoiding difficulties of MCMC such as sufficient mixing diagnostics. A good description and links for further information on VB and EP can be found in M. Seeger's corresponding research page. |
Monte-Carlo Gaussian variance estimation
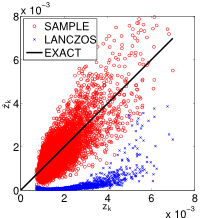 |
Some of the most successful variational approximation algorithms for large-scale problems are of a double-loop nature, requiring Gaussian variance estimation in the outer loop and standard sparse point estimation in the inner loop. The ubiquity of the Gaussian variance computation routine is not coincidental. Variational approximations try to capture uncertainty in the intractable posterior distribution along the directions of sparsity. These are naturally encoded in the covariance matrix of the proxy Gaussian variational approximation. In our work, we have demonstrated that estimating Gaussian variances by Monte-Carlo is particularly effective in this setup. This sample-based estimator works by first drawing samples from the Gaussian approximation, then employing the standard sample-based variance formula for estimating the variances. It is scalable to large-scale models, thanks to the efficient Gaussian sampling by local perturbations algorithm; see our Perturb-and-MAP page for further info. The Figure to the left demonstrates the efficacy of the proposed variance estimator compared to another general-purpose variance estimator based on the Lanczos iteration. |
Application: Blind image deconvolution
 |
We have employed these ideas to image deblurring, the problem of recovering a sharp image from its degraded blurred version. We consider both the non-blind variant of the problem, where we know the blur kernel, and the more challenging blind variant, where the blur kernel is unknown and also needs to be estimated. The case for the Bayesian treatment of the problem is more compelling in blind image deconvolution, since it allows recovering the blur kernel in a principled way by maximum likelihood. |
Software
Our software for variational inference with Monte-Carlo variance estimation has been integrated into H. Nickisch's excellent glm-ie open source toolbox for inference and estimation in generalized linear models (starting from v. 1.4).
People
George Papandreou (contact person)
Publications
-
G. Papandreou and A. Yuille,
Gaussian Sampling by Local Perturbations,
Proc. Int. Conf. on Neural Information Processing Systems (NIPS-10), Vancouver, B.C., Canada, Dec. 2010.
[pdf] [bib] [poster] -
G. Papandreou and A. Yuille,
Efficient Variational Inference in Large-Scale Bayesian Compressed Sensing,
Proc. IEEE Workshop on Information Theory in Computer Vision and Pattern Recognition (in conjunction with ICCV-11), Barcelona, Spain, Nov. 2011.
[pdf] [bib] [arxiv] [ICCVW talk slides]
Acknowledgments
Our work has been supported by the U.S. Office of Naval Research under MURI grant N000141010933; the NSF under award 0917141; the AFOSR under grant 9550-08-1-0489; and the Korean Ministry of Education, Science, and Technology, under the National Research Foundation WCU program R31-10008. This is gratefully acknowledged.
 can often be
represented as finite or infinite mixtures of Gaussians with the help of local
or distributed latent mixture assignment variables
can often be
represented as finite or infinite mixtures of Gaussians with the help of local
or distributed latent mixture assignment variables 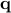 .
.